During my PhD years, I explored many projects in both physics and computer science. My main research focus is on the numerical simulation of quantum many-body system, using both the conventional stochastic methods and a novel semi-analytical method developed by our group.
Also, as a personal interest, I opened several side projects in computer science, mainly on the Machine Learning (ML), especially the methods/models related to Natural Language Processing (NLP), such as Transformer and BERT.
My current research interest is can be categorized as two directions [Click for more details]:
-
Keep working on the home-developed semi-analytical method to generalize to other systems and apply for more complicated observables.
- Incorporate more realistic interactions beyond the contact interaction to capture the corrections from the finite effective range, which is essential for the systems such as neutron matter.
- Further develop the formalism for more complicated observables:
- The near-term goals include the one- and two-body correlation functions, which are relevant to the quantities like the momentum distribution and the static structure factor.
- The mid-term goals are to include time evolution operator to investigate dynamic properties, such as the quantum quench process.
- In long term, I aim to generalize the method to study transport properties like bulk viscosity, and the dynamic structure factor, which requires a spatial-temporal, rather than purely spatial, two-body correlation function.
-
Explore ML-based techniques in the context of conventional stochastic methods, such as Quantum Monte Carlo (QMC) or Complex Langevin (CL)
Physics community is more and more open to machine learning and we are witnessing a rising trend towards incorporating the ML-based, state-of-the-art methods into the physics context.
Based on my experience in machine-learning related projects and the knowledge of conventional stochastic methods used for quantum many-body physics, I am especially interested in using ML-based techniques to assist the stochastic methods.
Though there are many successes in applying ML-based techniques to physics problem directly, it is not such a case for the simulation of quantum many-body systems in two aspects: a) the cost preparing training datasets amounts to that of running the simulation to the real problem directly. Fine-tuning the model to deal with different parameter configurations require extra costs, making it more attractive to apply the simulation to the real problem directly; b) The size of quantum state and the size of Hilbert space is much larger than the problems witnessing the success of machine learning. Such scaling up also require specially-tailored accomodations.
Therefore, I am more interesting in combining the benefits of stochastic methods and machine learning. In particular, I am investigating using transformer-based models and Physics-Informed Neural Network (PINN) to faciliate the random field generation, the most important and expensive step in the stochastic methods.
In other words, my goal is to design a more general random field generator, respecting physics laws and the symmetries, that can be applied in theoretically any systems. In this way, one can take advantage of the performance boosts from machine learning, without losing the generality of conventional methods.
Below is a selected list of projects I find may be interesting to share, though not all of them are published. Each project is given a color tag to indicate the status. There is also a Table of Contents tab on top for easier navigation.
Research in Physics
My research focuses on computational aspects of the quantum many-body
problem. In particular, I studied the so-called Unitary Quantum Matter, which include systems like ultracold atoms and the dilute neutron matter.
The “Unitary” refers to a special point, where the systems shows universality, i.e. different systems presents the same properties, as the there is only one (or a few) length scale govenrning the physics, so that all the other details become irrelavent. This is exactly how the two appearingly distinct systems, the low-energy atoms and the (relatively) high-energy neutron matter, are connected.
To this end, I investigated with two kinds of methods: the Automated Algebra Method developed by our group, and the conventional stochastic methods such as Quantum Monte Carlo and Complex Langevin as widely applied in various physics problems.
Automated Algebra Method
Most of my PhD research is on using the Quantum Virial Expansion (QVE) to analyze ultracold atoms under different settigs. The idea of QVE is to decompose the complicated many-body physcis into an infinite series of relative simple few-body problems, each of which can be described by a quantity called virial coefficient \(b_n\).
Now, the challenge is translated to accurately calculate \(b_n\) While \( b_2 \) was computed in 1937, it took more than 60 years to accurately determine \( b_3 \), due to the steep computational cost of quantum mechanics. In the past decade, researchers have been able to move on to \( b_4 \) , though the studies are limited to a very specific physics situation. Moreover, to determine \( b_n \) for higher-body systems, one need to deal with a delicated volume cancellations, which are easily disturbed by the statistical error as common in the conventional stochastic methods.
My work devotes to an novel, semi-classical method, named Automated Algebra (AA) method, which is free from statistical errors. The spirit of this method is to evaluate the matrix element of Boltzmann factor as analytical as possible, using a specially-tailored program that can conduct a very limited set of algebraic operation in an efficient fashion.
Virial Coefficient Calculation published
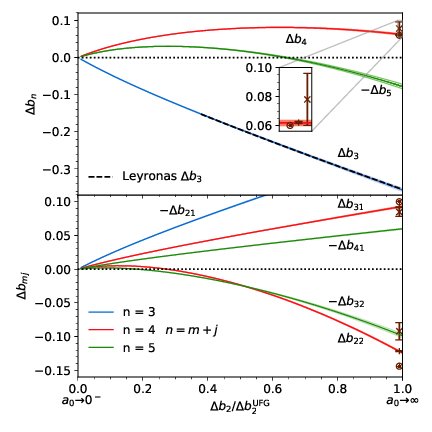
In the first paper along this research direction Phys. Rev. A 100, 063627 (2019), we developed the formalism and performed the calculation both in hand and by computer, laying down the foundation for the future work.
Followed by its publication, we greatly improved the formalism by incorporating particle symmetries and implemeted a Python program to perform the algebraic operations automatically. To further improve the efficiency, I developed the core computation modules in Cython and used multiprocessing libraries for parallelization. Afterwards, further parallelization is introduced to work on the Open Science Grid.
All these efforts lead to the second publication Phys. Rev. Lett 125, 050403 (2020), which is also selected as the Editors’ Suggestion. There, we determined \(b_4\) with high accuracy and agree very well with a conjecture, contributing to resolve the long-standing debate between theoretical estimations and experimental determinations.
The significance of our work is more than a benchmark. Thanks to the access to of higher-order coefficients, we can implement a technique called resummation to expand QVE’s convergence region, greatly improving the applicability of QVE. More importantly, our formalism is versatile and can be generalized to a wide range of systems and quantities, making QVE a candidate for more complicated investigations.
Thermodynamics and Tan’s contant in different systems published

Phys. Rev. Research 3, 033099 (2021)
Encouraged by the success, we further generalized the formalism and applied it to calculate multiple observables: density, pressure, Tan’s contact, susceptibility and compressibility. We also studied the homogeneous systems in different dimensions, which demonstrates a huge advantage of our method: the results are analytical expressiosn of parameters such as dimension, so that we do not need to rerun the calculation for different settings. This set of works was summarized in a follow-up publication Phys. Rev. A 102, 033319 (2020).
The latest work is to generalize this method to harmonically trapped system. Even the basic idea stays the same, there are significant changes to the formalism and the implementation details. This is because we need to use the coordinate space eigenstate for the trapped Hamiltonian, resulting in larger computational costs as the trick to detect volume cancellation only work in the momentum space.
In the trapped systems, w Phys. Rev. Research 3, 033099 (2021)
Search for pseudogap regime in the Unitary Fermi Gas published
In this collaboration with the group from TU Darmsdadt, in Germany, we studied the paring behaviour of the Unitary Fermi Gas in the normal phase, looking for signatures of
My work in this paper served as a benchmark for the results from conventional stochastic methods. Crucially, my results are smooth functions, as they are analytic expressions, and not only validate but also extend the stochastic results, which are discrete.
Static and Dynamic Structure Factor for Neutron Matter ongoing
In this project, I keep exploring the generalization of AA method.
With an acceptable error from the finite-range interaction, the dilute neutron matter can be approximated by the Unitary Fermi Gas under some conditions.
Dilute Neutron Matter with Finite-Range Interaction ongoing
Dilute neutron matter, as in the crust of a neutron star, belongs to the same universal class as
Stochastic Method
Quantum monte carlo in 2D trapped system unpublished
Energy of bosonic droplets unpublished
Enhanced Linear Solver for Complex Langevin Method ongoing
Machine-learning based random field generator ongoing
Projects in Computer Science
As a personal interest, I conducted a few research projects in computer science,
Quantum matter map ongoing
Enhanced attention mechanism using CNN on hold
In this project, I aimed to explore
COVID-19 event extraction from noisy tweets published
The result is published on In Proceedings of the Sixth Workshop on Noisy User-generated Text (W-NUT 2020), pp. 499-504. 2020
Undergraduate Research
Numerical simulation of acoustic field undergraduate
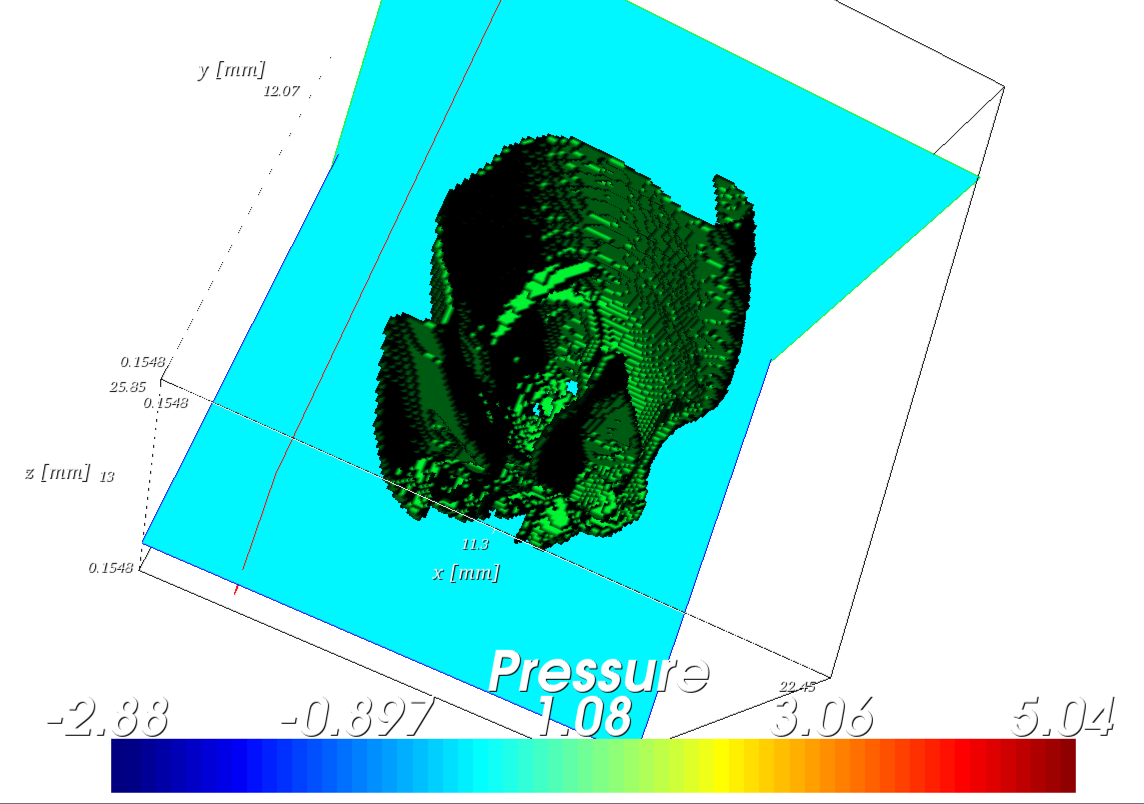
This project is my undergraduate thesis, supervised by Dr. Hongwang Lu. I developed a medium-scale C program to implement the Finite-Difference Time-Domain (FDTD) method for classical acoustic field, in order to study the propagation of acoustic fields through a bats’ ear, as well as to verify and explain how the significant geometric features of the bat’s ear contribute to its superior directional receiving ability.
Jamming and flow of granular material in a 2D hopper undergraduate

In my junior year, I had a chance to study at Duke University for one year (2013-2014), as part of a exchange program between Taishan College, Shandong University and Duke University. I am very honored to be able to worked in Prof. Robert Behringer’s group for undergraduate research, co-mentored by him and Dr. Joshua Dijksman, a then-postdoc and now-associate professor at Wegeningen University.
In the experiment, photoelastic disks were released in a 2D hopper, where both the size of the opening and the angle of supporting walls are controllable. Under deformation, the optical properties of photoelastic disks will change and therefore, after passing through the polarizing filter. To that end, a polarized light source was placed behind the hopper and a high-speed camera with polarizing filter in front, such that when a particle is deformed, the intensity captured will change accordingly. Placed at a slighly different angle in front of the hopper, a second camera without the filter was used to take the normal picture in synchronization with the first one.
I did NOT participate in the experiment, which was performed by Dr. Junyao Tang, who was a PhD student graduated in the previous year. My main job was two parts: Firstly, I perform image registation to align the images from two cameras, and then apply pattern recognization to the normal image to identify and locate each particle.
With these information, I can trace the particle in the polarized image, and then reconstruct the force field, and more ideally the stress tensor, for each of them. The latter part is difficult as the image contains only the intensity information. Using a quantity coined as Moment of Intensity, a different kind of MoI, which showed correlation to the stress tensor in a benchmark experiment, we successfully approximated the force field.
The ultimate goal is to discover the phase transition between the jamming phase and flowing phase, which is fundamental to the understanding of granular flow and has wide application in industries. Unfortunately, due to the limitation of time and knowledge at that time, I were not able to reach this part by the end of my exchange program.
Experiments on thermoelectric ceramics undergraduate published
I joined this project, which is also my first, during the second semester of the sophomore year (Spring 2013), as part of the Undergraduate Research Program. Suprevised by a PhD student Yi Li and his advisor Jian Liu, I helped with the preparation of thermoelectric ceramics, performed X-Ray Diffraction (XRD) measurements, and ran data analysis. I only participated in the early stage of this project and the result was later published at Scripta Materialia, 109, 80-83 (2015).